Mirandesa Breed Calves: Growth Performance and Carcass Characterization Affected by Sex and Livestock Production System
Sousa F, Lorenzo J.M, Vazquez J.A, Cantalapiedra J, Iglesias A, Franco D.
DOI10.21767/2572-5459.100001
Sousa, F.,1 Lorenzo, J.M.,2* Vazquez, J.A.,3 Cantalapiedra ,J.,4 Iglesias, A.,5 Franco, D.1,5
1Escola Superior Agrária, Instituto Politécnico de Bragança. Portugal
2Centro Tecnológico de la Carne de Galicia, Rúa Galicia No. 4, Parque Tecnológico de Galicia, San Cibrán das Viñas, 32900 Ourense, Spain
3Grupo de Reciclado y Valorización de Residuos (REVAL). Instituto de Investigaciones Marinas (IIM-CSIC), C/ Eduardo Cabello, 6, CP 36208, Vigo, Spain
4Farm Counselling Services. Consellería do Medio Rural, Xunta de Galicia, 27004, Lugo, Spain
5Departamento de Anatomía y Producción Animal. Universidad de Santiago de Compostela, 27002, Lugo, Spain
- Corresponding Author:
- J.M. Lorenzo
Tel: +34 988 548 277
Fax: +34 988 548 276
E-mail: jmlorenzo@ceteca.net
Received Date: September 21, 2015 Accepted Date: November 17, 2015 Published Date: November 23, 2015
Citation: Sousa F, Lorenzo JM, Vazquez JA, et al. Mirandesa Breed Calves: Growth Performance and Carcass Characterization Affected by Sex and Livestock Production System. J Anim Res Nutr. 2015, 1:1. doi: 10.21767/2572-5459.100001
Copyright: © 2015 Sousa F, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The effect of sex and livestock production system (LPS) on growth performance and carcass characteristics of Mirandesa breed calves was studied. A total of 2,263 and 60 animals for growth performance and carcass characteristics, respectively were used. Initially, the suitability of several equations to describe the growth of cattle from the Mirandesa variety was studied. In all situations, mathematical models were formulated with parameters of clear biological meaning. Bertalanffy and Gompertz equations were the most satisfactory equations to model the growth of males and females, respectively. Calves from traditional system were 68.61 kg heavier than animals from extensive system. On the other hand, calves from traditional systems showed (P<0.01) higher dressing percentage compared to animals from extensive system. There were significant differences for all morphometric parameters by LPS effect with the exception of internal depth pf chest, whereas sex effect had less importance. The LPS had statistically significant effect in all individual joints in the front quarter and hind quarter with the exception of sirloin and eye of round for front quarter and shoulder and the sum of chuck plus neck in the hind quarter. Finally, the LPS had statistically significant effect in all components of fifth quarter, with the exception of intestines, liver, tail and spleen, whereas sex effect only affected heart proportion.
Keywords
Mirandesa breed calves; Livestock
Introduction
The latest guidelines from the Common Agricultural Policy are based on benefit sustainable agricultures systems in opposition to intensive production system, because the use of local breeds has important advantages, as these breeds are closely related to the environment and they help to maintain biodiversity and sustainable agricultural production, especially in depressed areas. Concerning bovine breed reared in Mediterranean areas, they have received all approval from UE policy for above mentioned advantages and also for the possibility of commercialization under a label of Protected Designation of Origin (PDO) [1]. This is because consumer’s preference for traditional food is increasing since it assumed that those products are healthier and their quality is above-average [2]. In addition, the commercial value of traditional meat products, which are distinguished from nontraditional products in the market for their special production system provide added value to farmers; in this context in Portugal, veal production has been based on local native breed produced under semi-extensive conditions, where Mirandesa PDO veal is the most important commercial Portuguese veal with 247 carcass tons in 2007 [3].
Nowadays, the main destiny of Mirandesa breed is to produce meat and the livestock production system is mainly focused on small family farms, using indoor systems or traditional grazing in small scale family-farm systems. The production system aims to sell calves at weaning that occurs the ages of 5-8 months, which is the product demanded by industrials, butchers and supermarkets retailer [4].
In traditional system, the calves are raised on familiar farms with mother-cows, which have a period of milk feeding at least seven months. The calves are kept indoor all time and are fed in the morning and afternoon. The mother cows graze on natural pastures. They are collected overnight in traditional facilities (usually under the house of the farmer). In this system, calves are slaughtered at weaning, that occurs between 6-8 months of age. Apart of mother´s milk, their diet is supplemented with corn, potatoes, concentrates, corn silage and forages produced in the familiar exploitation. On the other hand, in extensive system, calves are raised outdoor, they accompany to the mothers grazing. Calves are weaned at different ages and when it is occurs, they are finished for a period between 2-4 months (indoor) with commercial feedings (should be of plants, predominantly cereals9 authorized by the PGI, oat hay and straw. To our knowledge, for Mirandesa breed no studies on growth of calves to weaning or adulthood exist and a few works on carcass characteristics are in the literature [5-7].
First of all, bovine meat production should be evaluated according to growth and carcass performance, and due to there is a solid agreement among UE politicians, farmers, researchers and final consumers on the necessity of gathering information concerning of native breeds, in the present work we propose a complete study of calf growth in both sexes of Mirandesa breed, using growth curves and estimates of weight at maturity by nonlinear growth models and the evaluation of carcass characteristics under the two most common livestock production systems (traditional and extensive).
Materials and Methods
Animal material for growth modelling
All animals of the present study are registered in the Record of Births of Stud-Book from Mirandesa breed. Calves were reared in traditional and extensive conditions under control of Protected Origin Label (DOP) from Mirandesa Association. This study used a total number of 2,263 animals (791 and 1,472 for traditional and extensive system, respectively) from 40 farms. A total of 5,243 live weight (LW) data were obtained between birth day and the 487 day of live for both sexes between 2003 and 2008. All calves were weighted by association technicians using an electronic bascule (TRU TEST, Almada, Portugal) with capacity up to 1,000 kg with a precision of 100 g and error of 1%. Animals were weighed every 2 months using the protocol previously mentioned.
Animal management and carcass measurements
For carcass characterisation a total of 60 calves (40 and 20 for traditional and extensive system, respectively; 37 males and 23 females) of the Mirandesa breed were used. Calves were slaughtered at 7.4 months. Animals were fasted from previous day of slaughter and they were transported from Malhadas (Portugal) the day of slaughter at 8:00 AM to an accredited abattoir in Miranda de Douro (NW Portugal) located at a distance of 8 km. All animals were slaughtered not later than 10:30 AM and hot carcass weight (HCW) was registered. Cold carcasses were weighed (CCW) after the refrigeration period (24 h at 0 ºC). At this point the following carcass measurements were made: length of carcass (LC), length of leg (LL), width of leg (WL), internal depth of chest (IDC) and perimeter of leg (PL) according to de Boer et al. [8]. In addition, carcass compactness index (CCI)=(CW/LC) and hind-limb compactness index (LTI)=(LL/WL) were calculated. The fifth quarter was weighed using an electronic bascule (TRU TEST, Almada, Portugal) with capacity up to 50 kg with a precision of 100 g. Blood amount from animals was not measured. LW corrected (LWC) was quantified as: LW at slaughtered day (kg) - [Weight full gastric reservoir (kg) - Weight empty gastric reservoir (kg) - Weight full intestines (kg) - Weight empty intestines (kg)]. Dressing percentage corrected (DPC) was defined as: (CCW/LWC) x 100. Chilling losses (%) were calculated as: 1 - [(CCW/HCW)] x 100
At 24 hour postmortem, the longissimus thoracis (LT) muscle was extracted between 6th and 10th rib. In both sides of the muscle (6 and 10 ribs) dorsal perimeter was drawn over acetate paper with a marker. Then, area in cm2, large (cm) and width (cm) was measured with the software Image Analyst using a photo of muscle.
Mathematical and Statistical Analysis
Calf growths modelling
The prediction of calf live weight growths until weaning was initially performed by means of linear, quadratic, logarithmic and logistic equations. In addition, the following exponential equation was also evaluated:
G = exp(a+ bt) (1)
where, G is the calf live weight growth (kg), t is the animal age (days), a is a dimensionless parameter associated with the initial weight of calves (G0) by the expression a=lnG0 and b is a parameter related to the specific growth rate (days-1).
Modelling of complete calves growths
The complete curve of live weight growth was modelled to three non-linear equations (Brody, Logistic, Bertalanffy and Gompertz) for comparison and selection of the best option. Two of these models (Logistic and Gompertz) are mathematically defined to describe mainly sigmoid profiles, Brody is only adequate for hyperbolic trends and Bertalanffy is indicated for both tendencies. Table 1 summarizes these equations.
| Equation | Reparameterised expression | Parameters of interest |
|---|---|---|
| Brody [2] |  |
 |
| Logístic [3] |  |
  |
| Gompertz [4] |  |
  |
| Bertalanffy [5] |  |
  |
G: Calves live weight, kg; t: Time from birth or animal age, days; Gm: Mature weight, kg; Τ: Time or age required to reach 50% of maximum live weight, days; μ: Specific live weight rate, proportion days-1; μm: Specific maximum live weight rate, days-1; b: Ratio between maximum calves live weight and birth weight, dimensionless; ti: Time or age at inflection point, days; vm: Maximum live weight rate, kg days-1; tm: Time or age required to achieve the beginning ofasymptote phase (Gm), days; λ: Lag phase of live weight, days
Table 1: Equations studied to model the live weight growth data of Mirandesa breed and parameter definitions with corresponding units.
Numerical methods and statistical analysis
Fittings to nonlinear equations were performed by minimisation of the sum of quadratic differences between observed and predicted values, using the non-linear least-squares (quasi- Newton) method provided by the macro ‘Solver’ of the Microsoft Excel spreadsheet. Estimation of confidence intervals (Student’s t test), consistence of equations (Fisher’s F test) and residual analysis (Durbin-Watson test) was also executed using the “SolverAid” macro, which is freely available from the Levie's Excellaneous website: https://www.bowdoin.edu/~rdelevie/ excellaneous/. Two criteria based on the information theory [9], Akaike information criterion (AIC) and Bayesian information criterion (BIC), were used to compare the predictive ability of non-linear equations to model calves growth data [10,11]:
 (2)
(2)
 (3)
(3)
The model with the lowest AIC and BIC is the one with the highest likelihood of being correct. The probability (Pr) of the chosen model being correct between two models m1 and m2 (pairwise comparison) can be calculated as indicated below:
 (4)
(4)
 (5)
(5)
Both probabilities vary in a range from 0 to 1 where the maximum probability to select the best equation is 1. Furthermore, bias and accuracy factors of data fitting to the non-linear equations were also calculated [12]:
 (6)
(6)
 (7)
(7)
Where log (predicted/observed) is the logarithmic relation between the predicted and the experimental values, and n is the number of data. The nearer the values of Bf (bias factor) and Af (accuracy factor) to 1 indicate the better the fitting of the models to experimental data. A value of 1 indicates that there is perfect agreement among predicted and observed data.
The covariance analysis of the fixed effects on growth kinetics by age mother at birth and inbreeding covariates was also performed by means of quadratic sum of type III using the General Linear Model (GLM) and Bonferroni Test for the multiple average comparison. The data treatment was done with SPSS package (SPSS 17.0.2 and 18.0.0, Chicago, IL, USA):
 (8)
(8)
where, Gijklmna is the growth or life weight; Sxi is the sex fixed effect (i=1 - male, 2 - female); Stj is the production system fixed effect (j=1 - extensive, 2 - traditional); Zok is the production council fixed effect (k=1 - Bragança, 2 - Vinhais, 3 - Macedo de Cavaleiros, 4 - Vimioso, 5 - Miranda de Douro, 6 - Mogadouro, 7 - Évora, 8 - Portoalegre); Fal is the parity of the mother fixed effect (l=1 - 1º birth,…, 12 - 12º birth); Exm is the season of birth fixed effect (m=1 - winter, 2 - spring, 3 - summer, 4 - autumn); (SxFa)il is an interaction term; X1 is the age covariate in the day of weighing; X2 is the inbreeding covariate; nβ1 is a coefficient of regression; oβ2 is a coefficient of regression and εijklmna is the residual random error associated with the observation.
For the variability analysis of the growth, we used a univariate linear mixed model with maternal effect and the following fixed effects: production system (2 levels), sex (2 levels), breeding number (2 levels), council (8 levels), number of mother parity (14 levels), birth season (4 levels), mother age in the day of weighing (covariate), inbreeding coefficient (covariate). As random effects: the animal (56,128 cases) and the direct and permanent maternal effects (56,128 cases). The calculation of the parameter estimates, using the restricted maximum likelihood method [13], was performed by means of the variance components estimation procedure [14,15].
For the statistical analysis of the results of carcass quality, first of all it was performed an exploratory analysis of the data with the box plot in order to verify the existence of outliers. Data were studied for each parameter using Shapiro-Wilks test normality and Cochran test for homogeneity of the parameter variances. After an analysis of variance (ANOVA) using the General Linear Model (GLM) procedure of the SPSS above described was performed for all variables considered in the study.
When we studied the effect of the effect of sex and livestock system production on carcass parameters, fixed effect of sex and livestock system production was included in the model. The model used was:
 (9)
(9)
where: Yij is the observation of dependent variables, μ is the overall mean, Si is the effect of sex, Lj is the effect livestock system production, (SL)ij is the interaction terms between sex and slaughter age and εij is the residual random error associated with the observation.
Results and Discussion
Mirandesa calf live weight growths from birth until wearing
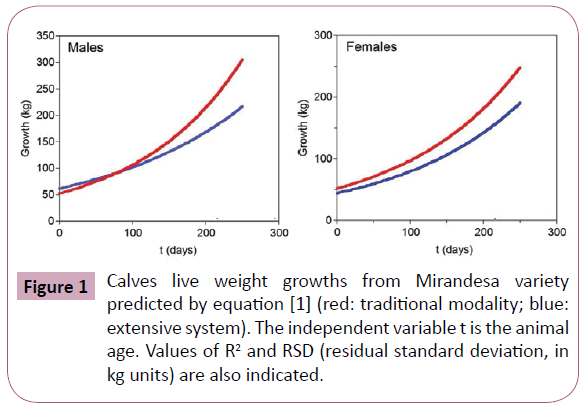
The data of calves were fitted to different equations: linear, quadratic polynomial, logarithmic, logistic and exponential (1). The best fittings were obtained by equation (1) (data not shown). The parameter estimates and determination coefficients were: a=3.964, b=0.007, R2=0.929 for males growing under traditional system; a=4.122, b=0.005, R2=0.771 for males growing under extensive system; a=3.951, b=0.006, R2=0.884 for females growing under traditional system and a=3.794, b=0.006, R2=0.732 for females growing under extensive system. The simulated profiles of calves growths employed those numerical parameters are displayed in Figure 1.
The average daily weight gain (ADG) among birth and wearing under traditional system for males was 1.008 kg/day and 0.620 kg/day for extensive system. Carolino [16] found an ADG of 0.854 kg/day for Alentejana breed. The differences on growth between production systems were observed from 100 days and 70 days for males and females, respectively. Most likely at this age begin to observe the differences caused by careful feeding management that the breeders of the traditional production system dispense to his cows and calves. Similar differences among sexes were also obtained independently of production system from three months of birth. This observation is in agreement with the results reported by Preston and Willis [17] that did not observed the effect of the sexual hormones until the three months.
A previous study with a group of 17 calves from Mirandesa breed, had already indicated that milk production decreases from birth and that this reduction is increased from the three months of lactation. It is pointed out the sex is an important source of variation in animal weight between birth and weaning, and their influence is even more important when the weaning is later performed [18]. The differences among sexes found in the growth kinetics revealed that ADG for males is 0.224 kg/day higher than for females.
Complete growth of mirandesa calves until adult age
Experimental data of live weight growths for females and males calves were modelled by the equations described in material and method section. Parametric estimates and statistical analysis performed on the numerical fittings are summarized in Tables 2 and 3. All equations were statistically robust (P<0.001 from Fisher’s F test) and the parametric estimations were almost always significant (Student’s t test, α=0.05). The ability of the equations to predict the experimental data profiles were moderate with a goodness of fit range among 0.762-0.886. This statistical parameter was higher for females than males but the number of data in the asymptotic phase was low in both cases. The d-value from the Durbin-Watson test indicated a low autocorrelation among the residues. Moreover, the values of the bias and accuracy factors were always closed to one and therefore reaffirmed the validity of the equations assessed.
| Extensive males | Brody | Logistic | Gompertz | Bertalanffy |
|---|---|---|---|---|
| Gm (kg) | 520.5±122.8 | 257.5±11.1 | 296.6±19.8 | 325.4±27.8 |
| vm (kg days-1) | - | 0.826±0.035 | 0.790±0.035 | 0.783±0.037 |
| λ(days) | - | -33.5 (NS) | -42.6 (NS) | -45.1 (NS) |
| μm(days-1) | 0.0018±0.0006 | 0.0128±0.0009 | 0.0072±0.0007 | 0.0054±0.0007 |
| τ(days) | 343.7±117.1 | 122.5±8.6 | 146.2±15.4 | 167.0±22.2 |
| tm (days) | - | 278.4±18.8 | 282.1±28.7 | 578.4±72.7 |
| ti(days) | - | 122.5±20.0 | 95.5±10.7 | 78.1±11.6 |
| b | 0.933±0.013 | - | - | 0.509±0.013 |
| R2 | 0.7638 | 0.762 | 0.7642 | 0.7645 |
| Bf(bias factor) | 1.03 | 1.044 | 1.037 | 1.034 |
| Af (accuracy factor) | 1.219 | 1.229 | 1.221 | 1.219 |
| d (Durbin-Watson test) | 1.768 | 1.756 | 1.772 | 1.774 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 |
| Traditional males | ||||
| Gm (kg) | 6862 (NS) | 408.7±24.1 | 539.0±52.5 | 682.4±97.9 |
| vm (kg days-1) | - | 1.186±0.039 | 1.089±0.032 | 1.054±0.032 |
| λ(days) | - | 2.91 (NS) | -11.8 (NS) | -17.6 (NS) |
| μm(days-1) | 0.0001 (NS) | 0.0116±0.0006 | 0.0055±0.0005 | 0.0035±0.0004 |
| τ(days) | 4818 (NS) | 175.2±11.1 | 237.0±24.3 | 313.5±46.2 |
| tm (days) | - | 347.5±19.3 | 416.1±39.6 | 953.1±127.8 |
| ti(days) | - | 175.2±14.5 | 170.2±18.7 | 174.1±28.4 |
| b | 0.995 (NS) | - | - | 0.611±0.015 |
| R2 | 0.8759 | 0.8759 | 0.8791 | 0.8793 |
| Bf(bias factor) | 1.006 | 1.042 | 1.026 | 1.021 |
| Af (accuracy factor) | 1.175 | 1.184 | 1.17 | 1.167 |
| d (Durbin-Watson test) | 1.892 | 1.89 | 1.942 | 1.944 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 |
Table 2: Parametric estimations and confidence intervals (α=0.05) corresponding to the equations from Table 1 to model the live weight growth of Mirandesa cows males.
| Extensive females | Brody | Logistic | Gompertz | Bertalanffy |
|---|---|---|---|---|
| Gm (kg) | 358.1±52.5 | 226.6±8.5 | 250.6±19.8 | 267.4±18.0 |
| vm (kg days-1) | - | 0.754±0.033 | 0.735±0.035 | 0.737±0.038 |
| λ(days) | - | -36.1 (NS) | -43.3 (NS) | -44.5 (NS) |
| μm(days-1) | 0.0027±0.0006 | 0.0133±0.0009 | 0.0080±0.0007 | 0.0062±0.0007 |
| τ(days) | 225.7±54.3 | 114.1±7.4 | 128.2±12.0 | 140.6±16.1 |
| tm (days) | - | 264.4±16.7 | 251.4±23.0 | 500.6±74.8 |
| ti(days) | - | 114.1±10.4 | 82.1±8.1 | 63.0±8.1 |
| b | 0.911±0.011 | - | - | 0.493±0.013 |
| R2 | 0.8699 | 0.8727 | 0.8725 | 0.872 |
| Bf(bias factor) | 1.028 | 1.041 | 1.032 | 1.03 |
| Af (accuracy factor) | 1.223 | 1.238 | 1.223 | 1.221 |
| d (Durbin-Watson test) | 1.805 | 1.839 | 1.837 | 1.83 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 |
| Traditional females | ||||
| Gm (kg) | 6824 (NS) | 283.1±14.3 | 370.3±35.4 | 462.9±67.3 |
| vm (kg days-1) | - | 0.974±0.027 | 0.908±0.022 | 0.885±0.021 |
| λ(days) | - | -14.2 (NS) | -25.1 (NS) | -29.2 (NS) |
| μm(days-1) | 0.0001 (NS) | 0.0138±0.0008 | 0.0067±0.0007 | 0.0043±0.0006 |
| τ(days) | 5547 (NS) | 131.1±8.7 | 180.0±21.1 | 237.9±40.0 |
| tm (days) | - | 276.5±16.7 | 327.7±35.4 | 760.0±115.8 |
| ti(days) | - | 131.1±15.0 | 124.9±15.8 | 125.9±24.0 |
| b | 0.995±0.022 | - | - | 0.573±0.017 |
| R2 | 0.8835 | 0.8856 | 0.8858 | 0.8854 |
| Bf(bias factor) | 1.012 | 1.026 | 1.019 | 1.027 |
| Af (accuracy factor) | 1.163 | 1.166 | 1.161 | 1.16 |
| d (Durbin-Watson test) | 1.955 | 1.991 | 1.994 | 1.988 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 |
Table 3: Parametric estimations and confidence intervals (α=0.05) corresponding to the equations from Table 1 to model the live weight growth of Mirandesa calves females.
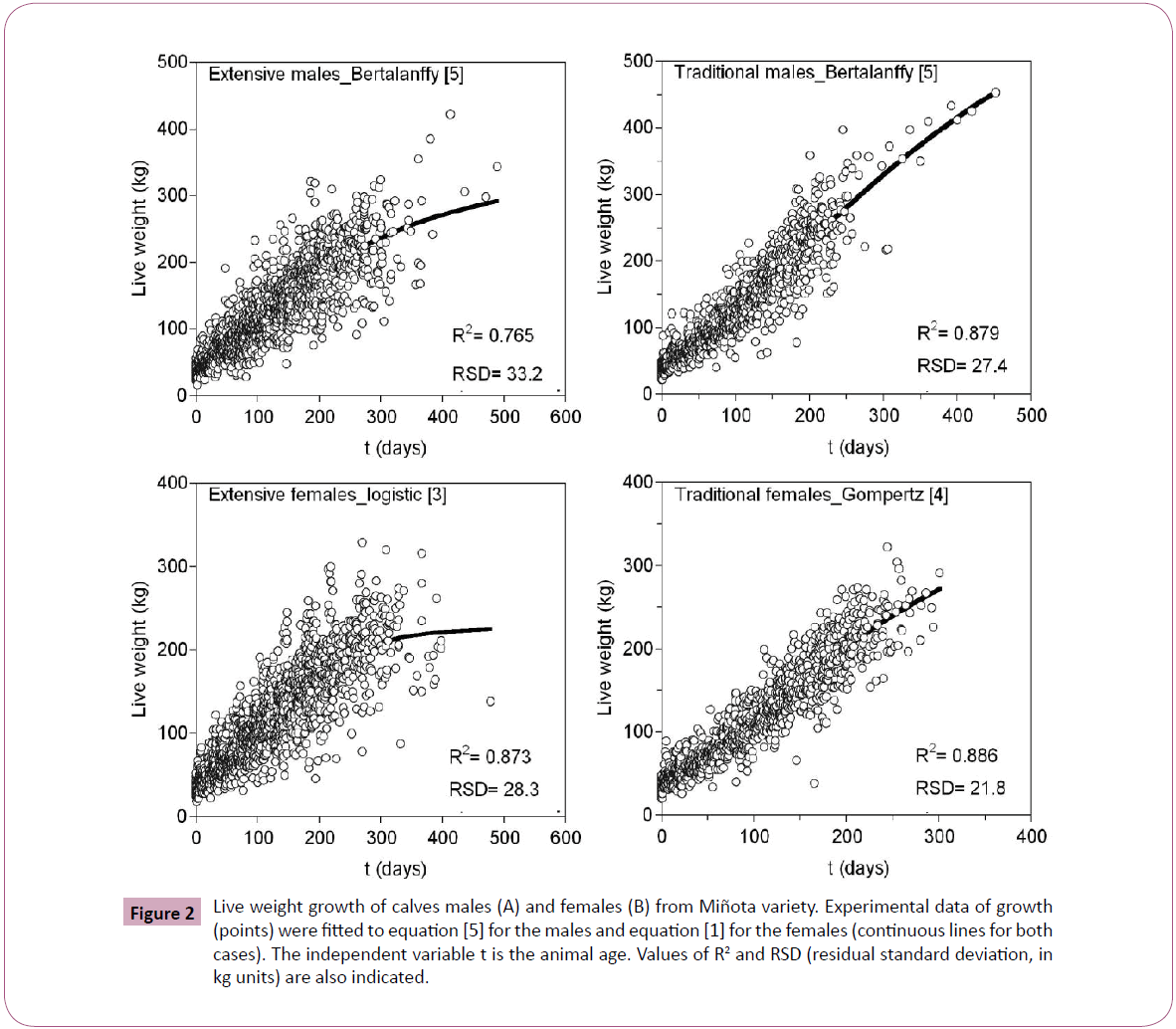
The most adequate equation to predict the growths were statistically compared using AIC and BIC methods. For male’s calves, the best option was equation (5) followed by (4) (PrAIC=1 and PrBIC=1). In the case of females, equation (3) for extensive modality and equation (4) for traditional system were the most interesting mathematical models to describe the growth data (PrAIC=1 and PrBIC=1). These results were also corroborated by the values of R2, Af and Bf. Experimental results of calves growths and corresponding description according to the equation (3) for females-extensive, (4) for females-traditional and equation (5) for males in both systems are depicted in Figure 2.
Figure 2: Live weight growth of calves males (A) and females (B) from Miñota variety. Experimental data of growth (points) were fitted to equation [5] for the males and equation [1] for the females (continuous lines for both cases). The independent variable t is the animal age. Values of R2 and RSD (residual standard deviation, in kg units) are also indicated.
In general the equations here evaluated are well-known tools for the modelling of animal growths when the environmental factors are stables and homogeneous during the time of growth [11,19]. Indeed, this condition is not met for growing cattle because feeding animals, management of production systems, diseases, etc., introduce alterations in the rate of growth at different stages of the life of animals [20,21]. In many growth descriptions, logistic and Gompertz equation was reported as the most suitable due to its fitting ability and biological meaning of parameters [11,21,22]. The lack of sigmoidity of the present growth data led to that equation (3) was more inaccuracy in comparison with the less sigmoid equation (5). Brody´s equation (2), although useful to simulate hyperbolic growth data, is inconsistent for application with another non-linear profiles and the number of parameters with biological or geometrical meaning is limited. Additionally, it presents difficulties to predict maximum growths (Gm) with low intervals of confidence (Tables 4 and 5) and underestimation of initial weights [19]. In this context, the sigmoid equations (3) and (4) and Bertalanffy (5) commonly overestimate the initial weights and underestimate the adult final weights [23,24].
| Variable | df | F | p-value |
|---|---|---|---|
| Sex | 1 | 149.49 | 0 |
| Council | 7 | 28.925 | 0 |
| Production system | 1 | 197.44 | 0 |
| Number of parity | 11 | 15.047 | 0 |
| Birth season | 3 | 29.209 | 0 |
| Inbreeding | 1 | 38.443 | 0 |
| Age weighted | 1 | 20495 | 0 |
| Number of parity × Sex | 11 | 3.035 | 0 |
Table 4: Results of covariance analysis for the fixed effects of factors studied that influence the live weight between birth and 456 days.
| System | Sex | SEM | P-Values | |||||
|---|---|---|---|---|---|---|---|---|
| Traditional | Extensive | Male | Female | System | Gender | System × Gender | ||
| Animals | 40 | 20 | 37 | 23 | ||||
| Age (days) | 221.9 | 223.4 | 222.5 | 222.2 | 2.2 | 0.584 | 0.754 | 0.125 |
| LW (kg) | 243.3 | 174.7 | 238.8 | 190.9 | 3.8 | <0.0001 | <0.0001 | 0.055 |
| LWC (kg) | 227.3 | 160 | 222.3 | 176.8 | 3.7 | <0.0001 | <0.0001 | 0.11 |
| HCW (kg) | 133.8 | 91.8 | 130.9 | 101.9 | 2.4 | <0.0001 | <0.0001 | 0.074 |
| CCW (kg) | 130.5 | 89.2 | 127.7 | 99.1 | 2.3 | <0.0001 | <0.0001 | 0.07 |
| DPC (%) | 57.3 | 55.5 | 57.3 | 55.9 | 0.3 | 0.009 | 0.082 | 0.324 |
| CL (%) | 2.5 | 2.9 | 2.5 | 2.8 | 0.1 | 0.085 | 0.283 | 0.722 |
Table 5: Mean, error and significance level of growth performance and carcass characteristic from calves of Mirandesa breed from both sexes reared in two livestock production system (traditional and extensive).
In general, the growth parameters of females (Gm, vm, τ and tm) were significantly lower (more than 30% based on Gm value) than the males for all equations tested (Tables 4 and 5). Similar outcomes were reported by other cattle breeds: Arouquesa [25], Alentejana [16] and Maronesa [26] as well as previous studies of Mirandesa variety [27]. The comparison between the two systems of production revealed, as in the case of calf’s live weight growths, the capacity of traditional modality for producing much higher growth parameters than extensive modality in both sexes.
Covariance analysis allowed to prove the fixed effect of various factors on live weight. The live weights analyzed ranged from 16 kg at birth and 453 kg at 456 days of life using 5,178 observations. Calves from cows with more than 12 births were excluded from that statistical analysis. Neither repeatability effect associated to the animals was taken into account. In general, significant effect was observed for all the factors evaluated (Table 4). Thus, the live weight growth was influenced by sex, council of birth, the type of production system, the number of parity, the birth season, the inbreeding as well as the joint effect of sex and number of parity.
Effect of livestock production system and sex on carcass characteristics
Table 5 presents the results of the carcass characteristics respect to LPS and sex. Calves were slaughtered at similar age (222 days; 7.4 months). There were significant differences for LWC between livestock production systems (LPS) and sexes. Calves from traditional system were 68.61 kg heavier than animals from extensive system. Regarding dressing percentage, calves from traditional systems showed higher DPC (1.79%; P=0.009) compared to animals from extensive system. DPC from calves in traditional system (57.32%) were in the range obtained by Piedrafita et al. [28] working with seven Spanish breed (range between 56.3 to 58.1%). Also, Arthur et al. [29] studying heavy calves breeds slaughtered at 15 months of age, such as Angus, Hereford and Charolais reported DP of 55.7%, 56.6% and 55.6%, respectively. Lower values of DP were found in rustic endangered cattle breed, such as “Asturiana de la Montaña” [30] or in male rustic Galician cattle breed slaughtered at 9 months of age (Cachena, Caldelá, Vianesa, and Limiá) with values close to 48% [31]. Alberti et al. [32], investigating different Spanish breeds, such as “Rubia Gallega” reported DP values above 60%. These authors employed genetically selected animals and an intensive finishing period.
Comparing with Portuguese breeds, DP was higher to those found in smaller breeds such as Arouquesa (53%), Barrosa (54%), Maronesa (55%) and Mertolenga (56%) slaughtered at LW of 300 kg and also higher compared to larger larger format Portugueses breeds such as Alentejana (55%), Mirandesa (58%) and Marinhoa (58%) slaughtered at LW of 400 kg. Simões et al. [7] have found in males Mirandesa breed with a LWC of 498 kg a DPC of 60.1%. To reach higher DP yields to 60% is necessary increase the slaughter weight, achieving DP of 62% and 63% for Mirandesa and Marinhoa, respectively when animals were slaughtered at 650 kg of LW [7]. Concerning sex effect, there were significant differences (P<0.001) in slaughter weight and carcass weight between sexes (222.27 vs. 176.80 kg for LWC and 127.74 vs. 99.07 kg for HCW). Obviously, this difference of 45.47 kg between sexes was because to the higher growth of males respect to females, due to increased muscle development.
Effect of livestock production system and sex on carcass conformation
Morphological measurements are depicted in Table 6. There were significant differences for all morphometric parameters by LPS effect with the exception of IDC, whereas sex effect had less importance. It can be noticed that carcass from traditional system were more length (LC of 104.52 vs. 97 cm; P<0.0001), thicker (WL of 19.17 vs. 17.55 cm; P<0.05) and compact (CCI of 1.24 vs. 0.91; P<0.001). Similar tendency was found when sex effect was studied with carcass longer, thicker and more compactness in males than in females, although we did not obtain significant differences. Among the other two measurements collected in the leg (LL and PL) it was found that the calves of the traditional system showed significantly (P<0.001) higher values compared to the extensive system. When comparing the sex, we found that males had higher LL and PL but had an equivalent to the females WL (18.71 vs. 18.50 cm; P=0.808). The LC of the animals of the present work were higher than those observed by Arthur et al. [29] in Charolais claves slaughtered at 281 days who reported values of 95.2 cm
| System | Sex | SEM | P-Values | |||||
|---|---|---|---|---|---|---|---|---|
| Traditional | Extensive | Male | Female | System | Gender | System×Gender | ||
| Animals | 40 | 20 | 37 | 23 | ||||
| LC (cm) | 104.52 | 97 | 103.4 | 99.78 | 0.716 | <0.0001 | 0.083 | 0.851 |
| LL (cm) | 64.43 | 61.82 | 64.27 | 62.43 | 0.375 | 0.001 | 0.019 | 0.08 |
| PL (cm) | 86.31 | 78.8 | 85.25 | 81.47 | 0.572 | <0.0001 | 0.034 | 0.239 |
| IDC (cm) | 27.83 | 28.8 | 27.95 | 28.47 | 0.254 | 0.113 | 0.688 | 0.191 |
| WL (cm) | 19.17 | 17.55 | 18.71 | 18.5 | 0.223 | <0.0001 | 0.808 | 0.673 |
| CCI | 1.24 | 0.91 | 1.22 | 0.98 | 0.019 | <0.0001 | <0.0001 | 0.053 |
| HCI | 3.37 | 3.54 | 3.44 | 3.39 | 0.034 | 0.008 | 0.243 | 0.795 |
| 6th area (cm2) | 30.47 | 23.58 | 30.6 | 24.27 | 0.81 | 0.001 | 0.001 | 0.74 |
| 10th area (cm2) | 51.85 | 42.73 | 52.19 | 43.38 | 0.95 | <0.0001 | <0.0001 | 0.475 |
Table 6: Mean, error and significance level of carcass conformation characteristic from calves of Mirandesa breed from both sexes reared in two livestock production system (traditional and extensive).
CCI was significantly (P<0.0001) higher in carcass from males grew in traditional system compared with females in extensive system. This finding could be associated to higher carcass weight higher in traditional system and in males [33]. Concerning HCI, there were no significant differences in the transverse longitudinal index of the leg for sex effect. However, HCI was significantly (P<0.0001) higher in extensive groups, so legs of calves from the extensive system had a better compactness ratio than the legs of calves from the traditional (Table 6).
The importance of measuring the longissimus thoracis area already was indicated by Martin et al. [34], who observed that this parameter was high correlated with the carcass classification and dressing percentage, so it could be used to determine the muscular carcass growth [35]. It can be noticed that the longissimus thoracis area was greater in males than females, which indicates a higher muscular development and hence better conformation. However when we introduce carcass weight as a co-variate, there were no significant different between sexes for 10th rib (P=0.81) or the 6th rib (P=0.113). Similar results can be deduced when we compared between LPS, in general the LT area increase, as the calves grows which indicates an improvement in the conformation with age and/or live weight [36]. Comparing our results with those published for other breeds, Arthur et al. [29] obtained values at the 10th rib of 55.2 cm2 for Charolais calves.
Effect of livestock production system and sex on carcass composition
Front and hind quarter as a proportion of the carcass side and the proportions of the individual FQ and HQ joints are depicted in Table 7. The LPS had statistically significant effect in all individual joints in the FQ and HQ with the exception of sirloin and eye of round for FQ and shoulder and the sum of chuck plus neck in the HQ. On the contrary, sex effect had statistically significant effect on the proportionality of some individual joints in the FQ: sirloin, rump, topside, thick flank, silverside and hindshank and shoulder and chuck +neck were affected in HQ. HQ is the part of the carcass where several of the most valuable primal cuts are located, like loin, tenderloin, topside, silverside or eye of round. In this sense, there were significantly (P of 0.002 and 0.047) differences between sexes for HQ and FQ, respectively, whereas LPS did not affect (Table 7). A significant Pearson correlation between HCW (kg) and sum of all commercial cuts (kg) was found (r=0.98; P<0.001) and with most value commercial cuts named “Posta Mirandesa” in this area of Portugal (sum of sirloin, topside, thick flank, rump, silverside) (r=0.97; P<0.001). These results would be useful to predict the amount of most valuable primal cuts.
| System | Sex | SEM | P-Values | |||||
|---|---|---|---|---|---|---|---|---|
| Traditional | Extensive | Male | Female | System | Gender | System×Gender | ||
| Animals | 40 | 20 | 37 | 23 | ||||
| Front Quarter | ||||||||
| Loin | 7.56 | 6.13 | 7.27 | 6.87 | 0.132 | <0.0001 | 0.934 | 0.078 |
| Sirloin | 2.24 | 2.24 | 2.18 | 2.34 | 0.023 | 0.577 | <0.0001 | 0.773 |
| Rump | 3.8 | 4.03 | 3.81 | 3.98 | 0.031 | 0.001 | 0.024 | 0.621 |
| Topside | 7.23 | 7.75 | 7.24 | 7.68 | 0.061 | <0.0001 | 0.005 | 0.814 |
| Thick flank | 4.14 | 4.52 | 4.19 | 4.4 | 0.039 | <0.0001 | 0.043 | 0.747 |
| Silverside | 5.01 | 5.23 | 5 | 5.21 | 0.038 | 0.019 | 0.029 | 0.56 |
| Eye of round | 1.69 | 1.71 | 1.66 | 1.74 | 0.02 | 0.921 | 0.059 | 0.999 |
| Hindshank | 3.61 | 3.83 | 3.6 | 3.83 | 0.028 | 0.004 | 0.005 | 0.053 |
| HindQuarter | ||||||||
| Shoulder | 7.54 | 7.49 | 7.42 | 7.68 | 0.062 | 0.403 | 0.043 | 0.668 |
| Chuck+Neck | 9.97 | 9.5 | 10.22 | 9.21 | 0.084 | 0.084 | <0.0001 | 0.655 |
| Breast | 6.32 | 7.58 | 6.6 | 6.97 | 0.189 | 0.006 | 0.664 | 0.052 |
| Foreshank | 3.06 | 3.24 | 3.12 | 3.13 | 0.034 | 0.008 | 0.841 | 0.879 |
Table 7: Mean, error and significance level of carcass quarter (% respect to cold carcass weight) from calves of Mirandesa breed from both sexes reared in two livestock production system (traditional and extensive).
Effect of livestock production system and sex on fifth quarter composition
An important goal for the meat industry must be reduce the cost of fifth quarter disposal and improve returns. For meat industry, it would be desirable animals who present a maximum proportion of muscles, minimal of bone and offals and with a fat ratio desired for the market. But the reality is that the fifth quarter represents an average of 47% in beef tissues of total live weight (Walsh, 2014) or until 50% [37], where its edible components ranged between 16-18%. Before the onset of the BSE crisis and its consequent problems for the livestock sector, the available profit from the fifth quarter has been substantially eroded as markets were limited through export bans and much of the material from which value was once derived became no more than waste and a cost to the industry. A recently work has suggested that adopting fifth quarter practice could change a £100 charge per bovine into a £40 benefit per bovine [38], so possible recovery of the edible/ non edible components of the fifth quarter would be interesting.
Table 8 shows percentages values, respect to LW of the byproducts and offal of calves from Mirandesa breed. The LPS had statistically significant effect in all components of fifth quarter, with the exception of intestines, liver, tail and spleen, whereas sex effect only affected heart proportion (Table 8). It should be noticed that sum of head, skin and feet represent 17.29% and 16.83% respect to corrected live weight for males and females. This sum must be reduced to improve carcass yield, although skin percentage (range between 8.64-9.73%) was the most important byproduct, which also coincides with the highest appraisal and commercial interest for the meat producers. The percentage mean values of head (mean value of 4.82% for all systems) of this study were much higher than those observed by Simoes et al. [7] in different Portuguese breeds with extreme values of 2.40 to 2.81 for Alentejana and Mertolenga breeds, respectively. For Mirandesa breed, aforementioned authors found a mean value of 2.43%. Differences can be explained by the different maturity rates because of differences in slaughter age. The same explanation could be applied to the higher feet percentages in calves of our study, because aforementioned work [7] situated the feet percentage in a range between 1.79 to 2.15%.
| System | Sex | SEM | P-values | |||||
|---|---|---|---|---|---|---|---|---|
| Traditional | Extensive | Male | Female | System | Gender | System×Gender | ||
| Animals | 40 | 20 | 37 | 23 | ||||
| Skin | 9.73 | 8.64 | 9.62 | 9.01 | 0.175 | 0.01 | 0.356 | 0.13 |
| Intestines | 5.88 | 5.34 | 5.89 | 5.39 | 0.124 | 0.09 | 0.161 | 0.25 |
| Head | 4.45 | 5.37 | 4.71 | 4.78 | 0.062 | <0.0001 | 0.594 | 0.381 |
| Stomachs | 2.39 | 4.46 | 2.73 | 3.57 | 0.142 | <0.0001 | 0.12 | 0.078 |
| Feet | 2.83 | 3.33 | 2.96 | 3.04 | 0.031 | <0.0001 | 0.827 | 0.574 |
| Liver | 1.58 | 1.6 | 1.59 | 1.62 | 0.025 | 0.205 | 0.533 | 0.637 |
| Lung | 1.66 | 1.41 | 1.67 | 1.43 | 0.041 | 0.019 | 0.051 | 0.078 |
| Heart | 0.48 | 0.54 | 0.47 | 0.55 | 0.008 | 0.001 | <0.0001 | 0.051 |
| Tongue | 0.39 | 0.46 | 0.41 | 0.41 | 0.011 | 0.003 | 0.638 | 0.689 |
| Tail | 0.36 | 0.34 | 0.35 | 0.35 | 0.006 | 0.318 | 0.62 | 0.223 |
| Kidney | 0.28 | 0.36 | 0.31 | 0.31 | 0.009 | <0.0001 | 0.994 | 0.312 |
| Spleen | 0.25 | 0.27 | 0.27 | 0.23 | 0.011 | 0.129 | 0.075 | 0.16 |
| Intestine and stomachs are without gut content | ||||||||
Table 8: Mean, error and significance level of fifth quarter (% respect to live weight corrected) from calves of Mirandesa breed from both sexes reared in two livestock production system (traditional and extensive).
Regarding visceral organs, liver and heart are among ones with greater metabolic activity in calves [39]. Ferrel and Jenkins [40] also confirm that the heart and the lungs have high metabolic rates and, moreover have priority in using nutrients compared to the spleen and kidneys. In this work, there were significant differences, for the set of organs between LPS maybe due to the higher food restriction of calves in the extensive system. The mean percentage of visceral organs calculated as the sum of the lung, heart, liver, spleen and kidneys was 4.22%. Simoes et al. [7] working with seven Portuguese breeds found values for organs ranged between 3.69-4.08%, with a mean value of 3.75% for Mirandesa breed. As discussed, previously comparisons should be made with caution due to age differences generating allometric differences between different tissues besides slight methodological differences in the measurement procedures could exist.
Conclusions
The live weight growth data of Mirandesa variety were modeling by a set of non-linear equations. Bertalanffy equation for male’s calves and Gompertz for females were in general the best options to describe and predict growth data. Calves from traditional system showed a dressing yield higher in 1.79% than animal from extensive system and higher carcasses (>41 kg). Higher measurements for leg were obtained for traditional animals and males, so better carcass indices (CCI and HCI) were obtained respect to animal from extensive system and females, respectively. There were significant differences for total carcass fat between the production systems, showing an average of 1.95% more fat calves from traditional system than those obtained from extensive system.
References
- Costa P, Roseiro LC, Bessa RJB, Padilha M, Partidário A, et al. (2008) Marques de Almeida, J. Muscle fiber and fatty acid profiles of Mertolenga-PDO meat. Meat Science 78: 502-512.
- Hermansen JE (2003) Organiclivestockproductionsystems and appropriatedevelopment in relationtopublicexpectations. LivestockProductionScience 80: 3-15.
- Pestana JM, Costa ASH, Alves SP, Martins SV, Alfaia CM, et al. (2012) Seasonalchanges and muscletypeeffectonthenutritionalquality of intramuscular fat in Mirandesa-PDO veal. MeatScience90: 819-827.
- Sousa F, Sánchez L (2009) Mirandesa. Ed. Asociación de los Criadores de Bovinos de Raza Mirandesa.
- Simoes JA, Mira JFF(2002)Ageemptybodyweight and carcasscomposition at thesameproportion of total carcassfat in Portuguesecattlebreeds. LivestockProductionScience 74: 159-164.
- Simoes JA, Mendes I (2003) Distribution of tissues in carcasses at thesameproportion of total fat in Portuguesecattlebreeds. Animal Research 52: 287-298.
- Simoes JA, Mira JFF, Lemos JPC, Mendes IA (2005) Dressingpercentage and itsrelationshipwithsomecomponents of thefifthquarter in Portuguesecattlebreeds. LivestockProductionScience 96: 157-163.
- De Boer H, Dumont BL, Pomeroy RW, Weniger JH (1974) Manual on E.A.A.P. referencemethodsfortheassessment of carcasscharacteristics in cattle. LivestockProductionScience 1: 151-164.
- Shannon C. E (1948) A note onthe concept of entropy. Bell SystemTechnicalJournal 27: 379-423.
- Shi P, Tsai C (2002) Regressionmodelselection: a residual likelihoodapproach. Journal of Royal StatisticalSociety Series B2 64: 237-252.
- Vázquez JA, Lorenzo JM, Fuciños P, Franco D (2012) Evaluation of non-linear equationstomodeldifferent animal growthswith mono and bi-sigmoidprofiles. Journal of TheoreticalBiology 314: 95-105.
- Vázquez JA, Durán A, Rodríguez-Amado I, Prieto MA, Rial D, et al. (2011) Evaluation of toxiceffects of severalcarboxylicacidsonbacterialgrowthbytoxicodynamicmodelling. MicrobialCellFactories 10: 100-110.
- Patterson HD, Thompson R (1971) Recovery of inter-block informationwhen block sizes are unequal. Biometrika 58: 545-554.
- Neumaier A, Groeneveld E (1998) restrictedmaximumlikelihoodestimation of covariances in sparse linear models. GeneticsSelectionEvolution 30: 3-26.
- Groeneveld E, Kova M, Mielenz, N. VCE (2008) User’s Guide and Reference Manual Version 6.
- Carolino RN, Gama LT, Afonso FP, Rodrigues JS (1993) Curvas de crescimentoem bovinos de raça Alentejana e suarelaçãocom caracteres reprodutivos. Revista Portuguesa Ciência Veterinaria 508: 164-174.
- Preston JR, Willis MB (1970) Intensivebeefproduction. PergamonPress, Oxford, England (2ndedn).
- Bellido MM (1985) Influencia de ciertos factores ambientales sobre la productividad del ganado vacuno Retinto en la dehesa. INIA-MAPA, Madrid, Spain.
- Freitas AR (2005) Curvas de crescimentonaprodução animal. Revista Brasileira de Zootecnia 34: 786-795.
- Menchaca MA (1990) The Use of stagemodelsfordescribing animal growth curves. Cuban JournalAgriculturalScience 24: 31-36.
- Franco D, Crecente S, Vázquez JA, Gómez M, Lorenzo JM (2013) Effect of crossbreeding and amount of finishingdietongrowthparameters, carcass and meatcomposition of foalsslaughtered at 15 months. MeatScience 93: 547-556.
- López S, France J, Gerrits WJJ, Dhanoa MS, Humphries DJ, et al. (2000) A GeneralizedMichaelis-MentenEquationfortheAnalysis of Growth. Journal Animal Science 78: 1816-1828.
- Franco D, Vázquez JA, Lorenzo JM (2014) Growth performance, carcass and meatquality of the Celta pigcrossbredwithDuroc and Landracegenotypes. MeatScience 96: 195-202.
- Silva FF, Aquino LH, Oliveira AI (2002) Estimativas de parâmetros genéticos de curva de crescimento de gandoNelore (Bosindicus). Ciência e Agrotecnologia 26: 1562-1567.
- Mazzini ARA, Muniz JA, De Aquino LH, Fonseca E, Silva F, et al. (2003) Análise da curva de crescimento de machos Hereford. Ciência e Agrotecnologia 27: 1105-1112.
- Borges AJ (2000)Arouquesa. In: Catálogo de raças autóctonas de Castela e Leão (Espanha) -Região Norte de Portugal - I. Espécies bovina e equina. Garcia JEY Ed. Fundación ReiAfonsoHenriques.
- Alves VC (2000) Maronesa. In: Catálogo de raças autóctonas de Castela e Leão (Espanha) -Região Norte de Portugal - I. Espécies bovina e equina. Garcia JEY Ed. Fundación ReiAfonsoHenriques.
- Piedrafita J, Quintanilla R, Sañudo C, Olleta JL, Campo MM, et al. (2003) Carcassquality of 10 beefcattlebreeds of theSouthwest of Europe in theirtypicalproductionsystem. LivestockProductionScience 82: 1-13.
- Arthur PD, Hearnshaw H, Jonhoston D, Stephenson PD (1995) Evaluation of Angus, Charolais and Hereford as terminal sire breedsonHereford and first-crosscows. II. Carcassescharacteristics and retailyield of progeny. AustralianJournalAgriculturalResearch 46: 1245-1258.
- Vallejo M, Alonso L, Revuelta JR, Cima M, Cañon J (1991) Características de las canales de las razas bovinas asturianas. I. Bases cuantitativas de la valoración subjetiva. Archivos de Zootecnia 40: 335-357.
- Franco D, Fernandez M, Justo JR, Gonzalez L, GarciaFontán MC, et al. (2010) Carcasscharacterization of fourendangeredGaliciancattlebreeds. In 56th International Congress of MeatScience and Technology, Jeju (Korea), Aug 15-20.
- Albertí P, Ripoll G, Goyache, F. Lahoz, F. Olleta, et al. (2005) Carcasscharacterization of sevenSpanishbeefbreedsslaughtered at twocommercialweights. MeatScience 71: 514-521.
- Panea B, Olleta JL, Sañudo C, Campo CC, Piedrafita J, et al. (1999)Aspectos productivos y calidad de la canal en la raza-sistema Pirenaica. Efecto del peso al sacrificio. ITEA 20: 86-88.
- Martin TG, Alenda R, Cabrero M (1992) Carcasscharacteristics of Rubia Gallega and Asturiana cattle at 10 to 18 months of age. Journal Animal BreedingGenetics 109: 385-393.
- Garcia de Siles JL, Galvez JF (1976) Estudio comparative de las canals de terneros y añojos de las razas Frisón y Rubia Gallega. Zootechnia 25: 300-310.
- Hopkins DL, Roberts AHK (1995) Theevaluation of carcassweight, fatdepthmeasures and eyemuscleareaforpredictingthepercentageyield of saleablemeat in Australiangrass-fedbeefcarcassesforJapan. MeatScience 41: 137-145.
- Warriss PD (2004) MeatScience. AnIntroductory Text. Cabi Publishing.
- Walsh C (2014)The use of Animal By-products. Theimprovingopportunitiestoaddvaluetothebeef and sheepslaughteringsectors, EBLEX report.
- Smith NE, Baldwin RL (1974) Effects of breedpregnancy, and lactation, onweight of organs and tissues in dairycattle. Journal of DairyScience 57: 1055-1060.
- Ferrell CL, Jenkins TG (1998) Bodycomposition and energyutilizationbysteers of diversegenotypesfed a highconcentratedietduringthefinishingperiod: II. Angus, Boran, Brahman, Hereford, and Tuli Sires. Journal of Animal Science 76: 647-657.

Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences