Modeling the Age Difference between Humans and Felis catus Biological Cat Age: The Actual Age of a Cat
Rix Cambridge
DOI10.21767/2572-5459.100034
Rix Cambridge*
St. John Fisher College Arts and Sciences, East Ave Rochester, NY, United States
- Corresponding Author:
- Cambridge R
St. John Fisher College Arts and Sciences
3690 East Ave Rochester, NY 14618, United States
Tel: 5857506364
Fax: 5857506364
E-mail: masterstonestar@gmail.com
Received Date: July 31, 2017; Accepted Date: September 12, 2017; Published Date: September 18, 2017
Citation: Cambridge R (2017) Modeling the Age Difference between Humans and Felis catus Biological Cat Age: The Actual Age of a Cat. J Anim Res Nutr Vol No 2: Iss no: 2: 14. doi:10.21767/2572-5459.100034
Copyright: © 2017 Cambridge R. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
A new equation for converting cat years to human years was developed. This equation was created by taking current models and running regressions on them in order to make an equation that is more accurate. The new equation is a piecewise function of just a singular point and then a linear equation that grows to infinity. At x=1, the value is 16.6364. After that point and at x=1.5, the graph becomes linear following the equation y=4.134x+15.
Keywords
Cat Age; Developmental Biology; Linear Functions; Piecewise Functions; Regression
Introduction
The anatomy and physiology along with developmental biology of the domestic cat has provided evidence that the bodies of said organism develop at a faster speed than a human’s organs and other body parts. It is because of these developmental differences and biological differences that a feline would age faster than a human.
Background Information
The Domestic Cat is part of the Feliformia suborder within the Carnivora order. The Domestic Cat is further classified into the Felidae family and the genus of Felis. This gives the binomial name of the Domestic Cat to be Felis catus. A Cat's normal body temperature is 101.5Ãâ¹ÃÅ¡ F and some will not show discomfort until the skin approaches a temperature of around 126Ãâ¹ÃÅ¡ F. If water is available, then some Cats can tolerate temperatures close to 133Ãâ¹ÃÅ¡ F. The heart rate of the average domestic cat is between 120 bpm and 140 bpm and the average breathing rate is between 16 and 40 breaths per minute. Cats have minimal ability to sweat as the glands are located primarily in their paw pads. Instead, they pant for heat relief only at very high temperatures or if stressed. The average body temperature of a cat does not vary throughout the day as there is a lack of circadian rhythms. The urine excreted by the Domestic Cat is highly concentrated, allowing them to retain as much water as possible. Since their kidneys are so efficient, they can rehydrate by drinking seawater. Domestic Cats are able to swim, except they prefer not to as it leads to exhaustion quickly. The Domestic Cat has excellent night vision as they can see at one-sixth of the light level required for human vision. Unlike some big cats, the Domestic Cat has slit pupils in the eye. These pupils can focus bright light without chromatic aberration and are needed because the Domestic Cat’s pupils are much larger in relation to their eyes. At low light levels, the pupils will expand to cover most of the exposed surface of the eyes. Despite this, Domestic Cats have poor color vision and their eyes are optimized for sensitivity to blue and yellowish green colors. The Domestic Cat can detect an extreme broad range of frequencies. They can hear higher-pitched sounds than either dogs or humans. They can detect frequencies from 55 Hz to 79,000 Hz, about 10.5 octaves, whilst humans and dogs both have ranges of approximately 9 octaves. Compared to humans who have over 9,000 taste buds on the tongue, the Domestic Cat has about 470. The Domestic Cat, along with wild cats, share a genetic mutation that prevents them from being able to taste sweetness. To aid with navigation and sensation, cats have dozens of movable whiskers over their body, especially their faces. These provide information on the width of gaps and on the location of objects in the dark, both by touching objects directly and by sensing air currents; they also trigger protective blink reflexes to protect the eyes from damage. The neurological growth of the Domestic Cat is much faster than that of a human and thus there is a difference between the biological age of the cat and the age that it is referred to as.
Findings
Equation 1 was created by using the values given by a cat age conversion chart. This chart indicated that when we say that a cat is one-year old, it really means 15 years old for the cat. After the first year (when we say the cat is 2 years old), the cat would be 24 years old. From 2 years upward, the age of the cat increases by 4. This pattern led to the creation of equation 1, a piecewise function that covers this pattern. This equation has a special rule that goes along with it. In order for the pattern above to be true, a few rules have to be followed. First, take the age of the cat (for an example, a four-year-old cat). Take this age value and subtract two from it, this will be the x value. Then plug the remaining value into the piecewise function above to get the cat’s human age.
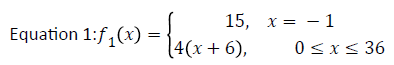
The piecewise equation above only takes into account full years. Therefore, it will only accept whole numbers being inputted. In order to get a more accurate conversion, the values produced by equation 1 were inputted into a TI-nSpire CX CAS calculator. This calculator helped to determine the linear, quadratic and cubic regression of the values calculated by the piecewise function. The y values were used to find the equation for the multiple linear regression. The equations that were produced as a variant of equation 1 helped obtain the final equation. Equation 2 was the equation that was produced by finding the multiple linear regression between the points given by equation 1. The age of the cat (so the age that is said) was placed on the x axis and the equivalent human age was on the y axis. The data plotted on this graph is located in Table 1. This regression produced an equation so similar to the regression that produced equation 3, equation 3 was discarded as it rounded the values.
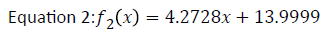
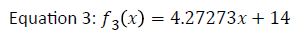
| X (Cat Age) | Y (Human Age) |
|---|---|
| 1 | 15 |
| 2 | 24 |
| 3 | 28 |
| 4 | 32 |
| 5 | 36 |
| 6 | 40 |
| 7 | 44 |
| 8 | 48 |
| 9 | 52 |
| 10 | 56 |
Table 1: Values on scatterplot.
Next, the quadratic and cubic regressions were determined. The quadratic regression (noted by equation 4) was found to match some of the values produced by equation 2, Table 2.
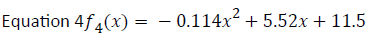
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| f1 | 15 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 |
| f2 | 18.2727 | 22.5455 | 26.8183 | 31.0911 | 35.3639 | 39.6367 | 43.9095 | 48.1823 | 52.4551 | 56.7279 |
| f4 | 16.9091 | 22.0909 | 27.0455 | 31.7727 | 36.2727 | 40.5455 | 44.5909 | 48.4091 | 52 | 55.3636 |
Table 2: Values produced by equations 1, 2 and 4.
The cubic regression produced an equation that gave values that did not match any of the already produced values. This value was rejected due to the belief that they would skew the overall new equation. Next, the x values of 1 through 10 were inputted into equations 1, 2 and 4 to produce y values for each input. Out of the three equations, equations 1 and 2 were chosen due to their representation of the lower end and the higher end of the age conversion. Table 3 shows the values produced by equations 1 and 2 for the x values 1 through 10. The values produced by equation 2 are rounded to the nearest whole number. The use of rounding here does not have a substantial effect on the produced values; it merely balances the significant figures.
| Cat Age (x) | Human Age Equivalent (y) | ||
|---|---|---|---|
| f1 | f2 | Rounded f2 | |
| 1 | 15 | 18.2727 | 18 |
| 2 | 24 | 22.5455 | 23 |
| 3 | 28 | 26.8183 | 27 |
| 4 | 32 | 31.0911 | 31 |
| 5 | 36 | 35.3639 | 35 |
| 6 | 40 | 39.6367 | 40 |
| 7 | 44 | 43.9095 | 44 |
| 8 | 48 | 48.1823 | 48 |
| 9 | 52 | 52.4551 | 52 |
| 10 | 56 | 56.7279 | 57 |
Table 3: Values produced by equations 1 and 2 with the values for equation 2 rounded.
In order to produce one set of values, the values from equation 1 and 2 were averaged together. The equation below shows how this works.
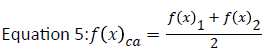
As an example, let the cat be said to be four years old. Equation 1 will produce a value of 32 at x=4 and Equation 2 will produce a value of 31.0911 at x=4. When these values are plugged into Equation 5, the result is 31.54555. This means that when the cat is said to be 4 years old, the cat is actually about 31.54555 years. In this equation, the values from equation 2 are not rounded. This equation uses the values from Table 3.
Values from x=1 to x=10 were plugged into the average equation in order to determine each y value. After the y values were found, the slopes of the points were compared. Between x=1 and x=2 the slope is different than the rest of the values. This result means that the final equation will be a piecewise function. Table 4 shows the values produced by this equation and the slope between each value set. The slope was calculated by the slope formula, and the slope was calculated between all points in order to make sure that the slope was constant. With a constant slope for x=2 all the way to x=10, this part of the equation (and graph) are linear.
| Cat Age (x) | Human Age 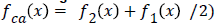 |
Slope (m) |
|---|---|---|
| 1 | 16.6364 | NA |
| 2 | 23.2728 | 6.6364 |
| 3 | 27.4092 | 4.1364 |
| 4 | 31.5456 | 4.1364 |
| 5 | 35.682 | 4.1364 |
| 6 | 39.8184 | 4.1364 |
| 7 | 43.9548 | 4.1364 |
| 8 | 48.0912 | 4.1364 |
| 9 | 52.2276 | 4.1364 |
| 10 | 56.364 | 4.1364 |
Table 4: Values produced by average equation and the slope between them.
It has been established that when it is said that a cat is 1 year old, the cat is actually 16.6364 years old. For years after 1, another partial equation is needed. The equation for the line greater than x=1.5 is: y = 4.1364 x + 15. Thus, with both this partial equation for values greater than and equal to 1.5 and with the value at 1, the final and most accurate equation can be
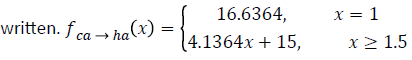
Conclusion
Cats mature and age faster than humans do. During the “first year” of a cat’s life it has matured at a speed that is faster than that of a human’s. In this “first year” of a cat’s life, it matures and grows to the equivalent of a 16.6364-year-old child. Even after the first year, the cat consistently matures and ages faster than a human. With a cat maturing faster than a human, saying the cat is 1-year old may be convention but in reality, the cat is older. Based on this new equational representation of the conversion, it is easier to now compute how old an individual’s pet cat is.
Future Direction
The main purpose was to create a more expansive equation to express the age that a cat is referred to and the actual biological age of the cat. The only foreseen expansion of this research would be to extend the bounds of the proposed equation in order to account for the ages of kittens.
Recommendations
It is recommended that the equation produced be used to accurately represent the biological age of the domestic cat. It is also recommended that this new equation be further extended to include the ages of kittens.
Appendix
Cat age: The actual biological age of a cat.
Human age: The age that the cat is referred to as.
Linear function: A function in the form y=mx+b. When graphed, the resulting image is a line.
Piecewise function: A function that is defined on a sequence of intervals.
Regression: A method for fitting a curve (not necessarily a straight line) though a set of points using some goodness of fit criterion. The most common type of regression is linear regression.
Cubic regression: A process by which the cubic (third degree) equation of “best fit” is found for a set of data.
Linear regression: A regression that is linear in the unknown parameters used in the fit. The most common form of linear regression is least squares fitting. Least squares fitting of lines are polynomials are both forms of linear regression.
Quadratic regression: A process of finding the equation of the parabola that best fits a set of data.
Acknowledgement
I would like to acknowledge Sophia Boreal for all of her support and encouragement throughout this research project and when writing the paper. She also helped with peer editing and offered important advice about formatting and grammar as well as which sources provided more valuable information.
References
- Expanded chart of cat age to human age2016.
- Marmot B (2016) Calculator cat.
- International cat care (2016) How to tell your cat's age in human years.
- Wolfram alpha LLC (2017) website encylopedia.
- MacDonald ML, Rogers QR, Morris JG (1984) Nutrition of the domestic cat, a mammalian carnivore. Annu Rev Nutr4: 521-562.
- Case LP(2003) The Cat: Its behavior, nutrition, and health. ames, IA: Iowa state university press.
- Subcommittee on dog, cat nutrition (2006) Nutrient requirements of dogs and cats. Washington, DC: National academies press.
- Kahn, Cynthia M, Line Scott (2007) Hollander, Joseph Lee, ed. The Merck/Merial manual for pet health. Merck.
- How do cats sweat? (2014) Cat Health.com.
- Adams T, Morgan ML, Hunter WS, Holmes KR (1970) Temperature regulation of the unanesthetized cat during mild cold and severe heat stress. J ApplPhysiol29: 852-858.
- Committee on animal nutrition (1986) Nutrient requirements of cats (2nd edn) National Academy Pr.
- Prentiss PG, Wolf AV, Eddy HA (1959) Hydropenia in cat and dog: Ability of the cat to meet its water requirements solely from a diet of fish or meat. Am J Physiol196: 625-632.
- Wolf AV (1959) Potability of sea water with special reference to the cat. Am J Physiol196: 633- 641.
- Fraser AF (2012) Feline behavior and welfare. CABI.
- Malmström T, Kröger RH (2006) Pupil shapes and lens optics in the eyes of terrestrial vertebrates. J ExpBiol209: 18-25.
- Hammond P, Mouat GSV (1985) The relationship between feline pupil size and luminance. Exp Brain Res59: 485-490.
- Loop MS, Bruce LL (1978) Cat color vision: The effect of stimulus size. Science 199: 1221-1222.
- Guenther E, Zrenner E (1993) The spectral sensitivity of dark- and light-adapted cat retinal ganglion cells. J Neurosci13: 1543-1550.
- Heffner RS (2004) Primate hearing from a mammalian perspective. Anat Rec A DiscovMol Cell EvolBiol 281: 1111-1122.
- Heffner HE (1998) Auditory awareness. ApplAnimBehavSci 57: 259-268.
- Christianne S, Do cats have a sense of taste?
- Why cats can't taste sweets. Petside.

Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences
